双曲线及其标准方程教案
教学目标
-
知识与技能:学生能够理解双曲线的定义,掌握双曲线的标准方程及其推导过程,并能运用标准方程解决相关数学问题。
-
过程与方法:通过观察、分析、归纳等方法,培养学生的逻辑思维能力和类比推理能力;体会数学转化思想在解决双曲线问题中的应用。
-
情感态度与价值观:激发学生学习双曲线的兴趣,培养学生勇于探索的精神和严谨的科学态度,感受数学美,提高学习数学的积极性。
教学重难点
-
重点
- 双曲线的定义及标准方程的推导。
- 双曲线标准方程的应用。
-
难点
- 如何从双曲线的定义出发,通过建系、列式、化简得到标准方程。
- 理解并掌握焦点在不同位置时,双曲线标准方程的变化。
教学方法
讲授法、讨论法、演示法相结合。
教学过程
-
课程导入(5分钟)
- 利用多媒体展示生活中一些物体运动的轨迹,如卫星绕地球运行轨道的一部分(双曲线弧段),引导学生思考这些轨迹的形状特点,引出本节课的主题——双曲线及其标准方程。
- 提问学生是否了解双曲线在日常生活中的应用,激发学生的学习兴趣和求知欲。
-
知识讲解(20分钟)
- 双曲线的定义讲解(8分钟)
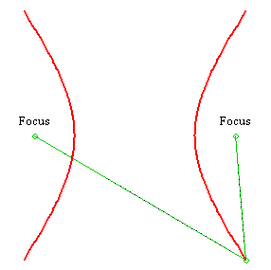
- 结合教材上的实例,给出双曲线的定义:平面内到两个定点(F_1,F_2)的距离差的绝对值等于非零常数(小于(|F_1F_2|))的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点之间的距离叫做双曲线的焦距。
- 用数学符号表示:设(||PF_1|-|PF_2||=2a (a\gt0)),2c)为焦距,且(2a\lt2c)。
- 双曲线标准方程的推导(12分钟)
- 以焦点在(x)轴上的双曲线为例进行推导,取过焦点(F_1,F_2)的直线为(x)轴,线段(F_1F_2)的垂直平分线为(y)轴建立平面直角坐标系(如图),设(M(x,y))是双曲线上任意一点,则(F_1(-c,0)),(F_2(c,0))。
- 根据定义可得(|MF_1|=\sqrt{(x + c)^2 + y^2}),(|MF_2|=\sqrt{(x - c)^2 + y^2}),因为(||MF_1|-|MF_2||=2a),所以有(\sqrt{(x + c)^2 + y^2}-\sqrt{(x - c)^2 + y^2}=\pm2a)。
- 接下来引导学生对上述等式进行化简,两边平方整理得((x + c)^2 + y^2=(x - c)^2 + y^2\pm4a\sqrt{(x + c)^2 + y^2}+4a^2),再次移项、化简并平方,经过一系列代数运算最终可得(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 (b^2 = c^2 - a^2)),这里(a\gt0,b\gt0),此即为焦点在(x)轴上的双曲线的标准方程,类似地,可引导学生推导出焦点在(y)轴上的双曲线的标准方程(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1 (a\gt0,b\gt0)),并强调两者的区别与联系。
- 双曲线的定义讲解(8分钟)
-
课件展示(10分钟)
- 通过动态演示双曲线形成的过程,让学生直观地观察到当点(M)满足到两个定点(F_1,F_2)的距离差的绝对值为非零常数(小于焦距)时,其运动轨迹形成双曲线,改变焦点的位置和距离差的常数值,展示不同情况下双曲线形状的变化,帮助学生加深对双曲线定义的理解。
- 利用课件展示双曲线标准方程的推导过程,将复杂的代数运算步骤分解呈现,便于学生理解和掌握,突出关键步骤和易错点,强化学生对推导过程的记忆。
-
课堂练习(15分钟)
-
布置一些与双曲线标准方程相关的基础练习题,如已知双曲线的焦点坐标和实半轴长,求双曲线的标准方程;或者已知双曲线的标准方程,求其焦点坐标、渐近线方程等。
- 求焦点在(x)轴上,且经过点(A(3,2)),实半轴长(a = 2),虚半轴长(b = \sqrt{5})的双曲线的标准方程。
- 已知双曲线的标准方程为(\frac{y^2}{9}-\frac{x^2}{4}=1),求它的焦点坐标和渐近线方程。
-
让学生独立完成练习,教师巡视指导,及时发现学生存在的问题并进行个别辅导,随后选取部分学生的答案进行展示和点评,针对出现的典型错误进行集体讲解和纠正,加深学生对知识点的理解和运用能力。
-
-
小组讨论(5分钟)
提出一个具有启发性的问题,如“如何根据双曲线的几何性质来判断其标准方程的形式以及相关参数的取值范围?”组织学生进行小组讨论,鼓励学生积极发表自己的见解和想法,培养学生的合作交流能力和自主探究精神,每个小组推选一名代表进行发言,分享小组讨论的结果,教师最后进行总结和补充。
-
课堂小结(5分钟)
- 引导学生回顾本节课所学的主要内容,包括双曲线的定义、标准方程的形式(焦点在(x)轴和(y)轴两种情况)以及标准方程的推导过程和应用,强调理解双曲线定义是推导和应用标准方程的基础,同时提醒学生在解题过程中要注意区分不同类型的双曲线及其相关性质。
- 询问学生是否还有疑问或不理解的地方,及时解答学生的问题,确保学生对本节课的知识点有一个清晰的认识。
-
作业布置(5分钟)
布置适量的课后作业,包括课本上的习题和一些拓展性的练习题,如让学生自己推导特定条件下双曲线的标准方程,或者应用双曲线知识解决实际生活中的问题(如某卫星的运行轨道问题等),以巩固所学知识,提高学生的综合应用能力。
教学反思
在教学过程中,要注重引导学生从直观感知到抽象思维的转变,通过多种教学方法帮助学生理解双曲线的定义和标准方程的推导,关注学生的个体差异,及时给予反馈和指导,鼓励学生积极参与课堂讨论和练习,提高学生的学习效果,在今后的教学中,可以进一步引入更多的实际案例和数学软件辅助教学,使教学更加生动形象,激发学生的学习兴趣和创新思维。
本文来自作者[贪恋繁华]投稿,不代表智博立场,如若转载,请注明出处:https://zhibor.cn/changshi/202503-25339.html


评论列表(4条)
我是智博的签约作者“贪恋繁华”!
希望本篇文章《双曲线的标准方程课件动态 双曲线及其标准方程教案》能对你有所帮助!
本站[智博]内容主要涵盖:知识科普
本文概览:双曲线及其标准方程教案教学目标知识与技能:学生能够理解双曲线的定义,掌握双曲线的标准方程及其推导过程,并能运用标准方程解决相关数学问题,过程与方法:通过观察、分析、归纳等方法,...